DPM集合論法則i Bra & i vy 景気回復理論の検証(調査)

最初に
2014年12.17 アッカーマン関数が連続して
組み合わせ爆発理論と重なり、
小さな素粒子が、今までにない
限界の限界を超えた、数段上のレベルに到達した。
SCG GROUP社の能力の器は
無限に広がった世界へと突き進んだ。
これが、SCG GROUP社の底力である。
時間配分能力・作業能力・叡智力・決断力・総合力...
新SCG GROUP社誕生を見て頂きたい。
アインシュタインの3つの歴史的論文
今から110年前、アインシュタイン博士は、3つの歴史的論文を発表した。
1905年 3月 光量子論
4月 ブラウン 論
6月 特殊相対性理論
18世紀から19世紀にかけてヨーロッパで起こった産業革命は、資本家と労働階級を生むという社会構造の変革をもたらし、
物理学的にも大きな影響を与えた。
産業革命の発端は、蒸気機関車の発明である。
熱から仕事への変換効率を上げるという工業的使命は、熱力学の研究を促し、
熱を原子・分子の運動として説明する気体分子運動論へと発展させた。
当時、原子・分子の存在は、実証されておらず、「実証されていないものは、
物理学的に取り入れるべきではない。」とする物理学者も多かった。
気体分子運動論の旗手ボルツマンは、反対者との論争に疲れ、1906年に自殺した。
しかし、だんだん原子・分子の存在を真剣に考える研究者も増えてきた。
その一人がアインシュタインであった。
19世紀 には、電気と磁気現象を統一した電磁気学がイギリスのファラデーやマクスウェルによって確立した。
これによって、電場と磁場が交互に振動し、空間を伝わることがわかった。
この現象が電磁波であるが、電磁波の伝わる速度は光の速度と一致し、光が電磁波であることが判明した。
しかし、音(波)が空気中を伝わるように、光が波なら、それを伝える媒質(伝達する物質)があるはずだ。
また、遠くの星の光は、真空の宇宙空間を伝わって地球に届く。
電磁器楽によれば、電磁波の速度は光源の速度に関係なく一定の値になっている。
それは何故なのか?
これらの疑問を抱き、アインシュタイン博士は特殊相対性理論の研究へと繋がっていくのである。
1905年3月 光量子論(プランクの発見)
1900年、富国強兵に励むドイツでは、鉄の生産効率を上げることが国策だった。
そのために溶鉱炉内の温度を正確に知る必要があった。溶鉱炉から漏れる光は、低温では赤いが、
温度から上がってくると黄色くなり、そして、白みを浴びてくる。
これは、溶鉱炉から出てくる光のスペクトルが自然に導かれることを示した。
一体何を意味するのだろう。
アインシュタインは、光電効果を例にとって、この意味を明らかにした。
光電効果とは、光を金属に当てると金属中の電子は、エネルギーを得て飛び出すはずである。
ところが、実際にある振動数以上の光を当てた場合にしか電子が飛び出してこなかったのである。
アインシュタインは、時仮をその振動数に比例したエネルギーを持つ粒子とすることによって、
この性質を見事に説明したのだ。
この光の粒のことを光量子という。
こうしてプランクの発見は、光の粒子性を意味することとなった。
この粒子と波の二重性の発見が、アインシュタインの量子論へと繋がっていく。
1905年4月 ブラウン運動
1827年頃、イギリスの植物学者ブラウンは、花粉を水に浮かべて顕微鏡で観測し、
花粉の中から飛び出した微粒子がいつまでもジグザグ運動を続けることを発見した。
この運動のことをブラウン運動という。
ブラウン自身は、この運動を生命体の源とみなそうとした。
しかし、花粉だけでなく水晶や硫黄などの微粒子でも同じような現象が起きていることが確認され、
生命現象とは何の関係もないことが明らかになった。
1905年4月、ブラウンが発見した花粉の粒子運動は、78年間の時が過ぎ
アインシュタインがジグザグ(ブラウン)運動の原因は、絶え間なく粒子に当たる水分子だと発表した。
大きな粒子の場合は、運動しないが小さな粒子の場合、活発に運動する。
粒子の大きさによって、運動が変化することを発表した。
これがアインシュタインの2つめの歴史的論文である。
1905年6月 特殊相対性理論
4月のブラウン運動に続いて、同年6月アインシュタインは「運動する物体の電気力学について」という論文を書いた。
これがいわゆる特殊相対性理論である。
アインシュタインは光が光源の速度によらず、常に一定の速度で伝わることと、
従来の力学での速度の合成則との矛盾に悩んでいた。
従来の速度の合成則は、「運動している車の進行方向にボールを投げると、
その速度は車の速度の分だけ速くなる。」という常識的には疑いようのないものであった。
アインシュタインは、一年間考え続けた末のある日の朝、目が覚めた時、この矛盾は解決していた。
「光の速さは、光源の運動によらず一定である。」という電磁気学の結果を原理(光速度不変の原理)として、
ニュートン力学とその基礎になっている時間と空間の概念に基本的修正を加えたのである。
すなわち、「動いている物体は止まっていたときよりも長さが縮み、時間の進みが遅くなる。」というのであった。
アインシュタインは、この理論の反響がすぐに現れていたが、この理論はあまりにも革命的過ぎて、
すぐに受け入れられなかった。
受け入れられないばかりか、激しく攻撃する物理学者もいた。
しかし、量子論の創始者プランクは、その価値をいち早く認め、
その結果、他の物理学者たちもだんだん特殊相対性理論に興味を持つまでになった。(相対性理論著書より)
アインシュタインのような物理学者の歴史的論文でさえ、「学説が正しい」と判断されるには、
アッカーマン関数を連続して用いて発表した論文でさえ、多くの論文を発表しても、
その時代(1905年代)では、爆発的な気流に乗らなかった。(SCG GROUP社)
アッカーマン関数
アッカーマン関数とは、とは、非負整数mとnに対し、
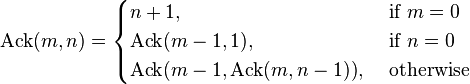
によって定義される関数のことである。
与える数が大きくなると爆発的に計算量が大きくなるという特徴があり、
性能測定などに用いられることもある。
再帰的な参照で表示している値は非常に大きく、
他の形式では簡単に表現することはできない。
アッカーマン関数は、経済にとっても重要な数式であり、
自然な形でその世紀事に大小問わず定義されてきた。
アインシュタインのような物理学者の歴史的論文でさえ、
アッカーマン関数を連続して用いて発表論文でさえ、
多くの論文を発表しても、爆発的気流には乗らない。
結果、組合せ爆発が最適化指数関数まで至らなかったということである。(SCG GROUP社)。
組合せ爆発(Combinatorial explosion)
組合せ爆発とは、主に計算機科学・応用数学・情報工学・人工知能などの分野では、
解が組合せ的な条件で定義される離散最適化問題で、問題の大きさnに対して
解の数が、指数関数や階乗などのオーダーで急激に大きくなり過ぎるために、
解あるいは、最適解を発見することが困難になることを言う。
つまり、物理学者アインシュタインの3つの歴史的論文発表
(1905年3月光量子論 4月ブラウン運動 6月特殊相対性理論)
は、発表期間があまりにも早すぎた結果、
「評価する側・研究者側・科学者側が「難しい論文」と位置付けてしまった。」結果である。(SCG GROUP社)
アインシュタイン教授の3つの歴史的論文は、アッカーマン関数と組合せ爆発を併用することで、
時流に乗ることができ、一般大衆生活者に早く広く社会貢献でき、
ノーベル物理学賞も、もっと早くに受賞できたと推測できる。(SCG GROUP社)
アインシュタイン教授は、アッカーマン関数論・組合せ爆発論を思慮しながら連続して発表したのか?
それとも、知らずに発表したのか?
舌を出して戯(おど)けた表情をするアインシュタイン教授の意図する目的は私には解らない。 (SCG GROUP社代表取締役 澤田浩一)
組合せ爆発論
組合せ爆発論には、通信ネットワーク・情報システム開発、化学その他の分野では、
より広義に、要素の数が多くなるとその組合せによって急激に、考えられる可能性の数、
とりうる実現形の数、実行すべき手順の数、あるいは、全体の複雑さが非常に巨大化してしまう理論もある。
組合せ爆発論には、計算量爆発が一般概念であり、指数的爆発もあり、
前述で述べているnの多項式オーダーで解ける計算式は、組合せ爆発とは言わない。
組合せ爆発の変わった例として、再帰的参照を含み急激に巨大化するアッカーマン関数がある。
情報システム開発では、解空間巨大化による計算量増大現象とは言い方が異なるが、
組合せ爆発が言われる。
その組み合わせで作られるシステムの複雑性は爆発的に膨張するので、
この問題への対応と解決は、情報処理の重要な課題である。

では、政治や経済はどうだろうか?
アッカーマン関数論と組合せ爆発論が経済景気回復システムとして時代気流していたのか?
経済大国第1位のアメリカ経済を検証してみよう。
next
アッカーマン関数と組合せ爆発の子細的説明につきましては、
日本訳あるいは、英訳での説明の用意もある。